Esprimi il rapporto fra apotema e lato dell'esagono con le seguenti approssimazioni:

1. A meno di 0,1
2. A meno di 0,01
3. A meno di 0,001

specificando, di volta in volta, se si tratta di un'approssimazione per difetto o per eccesso.

Ripercorriamo tutta l'attività che precedentemente abbiamo fatto a partire dal pentagono regolare, questa volta utilizzando l'esagono regolare.

Alcuni lavori degli alunni:

Lara

Jivini

Alessandro

Alessandro

Lara e Morgana

   Fig.1   Platycodum grandiflorus

ANNO SCOLASTICO 2014/15

L'anno scorso abbiamo già avuto modo di scoprire la relazione esistente fra la forma del guscio del mollusco Nautilius e la sequenza di Fibonacci. 

Quest'anno continueremo a ricercare la matematica nella natura... Cominciamo osservando il bocciolo di Platycodum grandiflorus:

• La sua forma è riconducibile ad un poligono regolare suddiviso in triangoli. Realizzalo con geogebra. 
• Documentati su questa specie floreale: quale forma assumerà il fiore dopo che sarà sbocciato? E il suo pistillo?
• Realizza con geogebra il fiore sbocciato

p.s.: Quanto prima porterò in classe la piantina di Platycodium grandiflorus

Fig.2 Bocciolo

Fig.3 Fiore sbocciato

• Quali poligoni compongono il bocciolo? E il fiore sbocciato?
• Quanto misurano gli angoli di ciascun poligono?
• Quali misure devi conoscere per calcolare l'area e il perimetro delle figure precedenti?

Osserva la figura seguente:

Fig.4 Pentagono stellato

Anch'essa ha al centro un pentagono regolare, ma i triangoli che formano le punte sono ottenuti in modo diverso.

                                                      Quanto misurano gli angoli di questa stella?

Ecco alcuni lavori degli alunni:

Tommaso F.

Lara

Giulia

Morgana

Misura con geogebra il lato di un pentagono e la distanza fra questo e il centro del pentagono (apotema),poi calcola il rapporto fra le due lunghezze, dilata la figura e calcola nuovamente il rapporto, ripeti questa azione più volte, riporta i risultati in una tabella.
Cosa osservi?

Il rapporto fra il lato del pentagono e quello dell'apotema è costantemente 1,45308.....
Il rapporto fra l'apotema e il lato del pentagono è costantemente 0,68819.....

• Perché tali rapporti sono costanti?

Questo triangolo è ottenuto con Excel. 

Apri una pagina di Excel o di Calc e  inserendo solo il numero 1 posto al vertice del triangolo, imposta tutte le operazioni  necessarie per inserire gli altri.

Complimenti a Lara, Tommaso e Morgana!
Ecco cosa hanno messo in evidenza:

(da Polymath)


La somma dei termini di ogni riga è:

 la successione delle potenze del 2. 

Si può anche dire che la somma dei termini di ogni riga è:

 il doppio della somma dei termini della riga precedente 

1. Adesso somma  i numeri che si trovano lungo ciascun segmento. Troverai una famosa successione. Quale?

1. Osserva attentamente la seguente figura ed inserisci negli esagoni i numeri mancanti:

2. Dopo aver inseriti tutti i numeri, somma quelli di ciascuna riga a partire dall'alto e otterrai una sequenza particolare:

1  2  4.........

3. Completa la sequenza.

4. Qual è la caratteristica di quell'insieme di numeri? E' possibile esprimere ciascun numero sotto forma di potenza mantenendo uguale la base? 

5. Questa successione di numeri ti richiama alla mente altri esempi incontrati in questo anno?

6. Sapresti continuare il disegno aggiungendo nuovi esagoni? Prova a realizzarlo con GEOGEBRA.

Il precedente disegno è noto come triangolo di Tartaglia

Niccolò Fontana (1499 - 1557) è stato un matematico italiano, al suo soprannome (Tartaglia), dovuto al suo linguaggio balbettante, è legato il noto triangolo numerico.

Richard Padovan, un architetto inglese contemporaneo, nel 1994 presentò in un saggio la seguente successione:

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, ...

1. Con quale criterio è stata costruita? Sapresti proseguire?
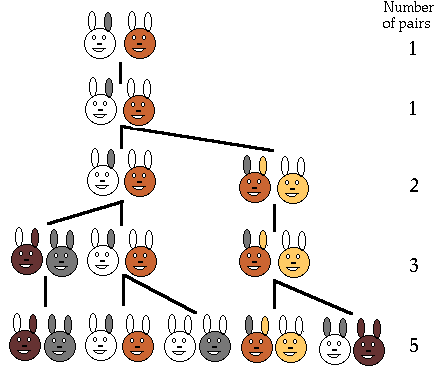
2. Osserva il disegno sottostante:

         Sai mettere in relazione la successione di Padovan con il disegno?

     3. Prova a continuare il disegno con la stessa logica, aggiungendo altri triangoli.

Riporto quanto scritto da Leonardo:

La sequenza è stata costruita con questo criterio: ogni numero si ottiene considerando i primi 3 numeri che lo precedono. Si sommano i primi 2 e si scarta il terzo Quindi dopo il 49 ci sarà 65, che si ottiene sommando i primi due numeri che procedono il 49 cioè 28+37=65 

Lara,  non solo ha rapidamente interpretato la successione e la relazione fra questa e il disegno, ma ha anche proseguito il disegno aggiungendo ulteriori triangoli!

4.  Adesso provate a realizzare lo stesso disegno con GEOGEBRA.

Un albero di Natale viene addobbato con luci di 4 colori che chiameremo per comodità: V (verde), R (rosso), A (arancione) e B (blu). La luce V si accende e si spegne ogni 2 secondi, la luce R si accende e si spegne ogni 3 secondi, la luce A si accende e si spegne ogni 5 secondi e la luce B si accende e si spegne ogni 6 secondi.

Rappresenta graficamente (con un disegno) il piano di accensione e spegnimento delle luci.                                    

Morgana, Filippo, Leonardo, Azzurra, Lara e Marco M. hanno immaginato al momento dell'accensione dell'interruttore (t= 0 sec)  tutte le lampadine accese.

Giulia le ha immaginate tutte accese dopo 1 secondo:

Marco R., Tommaso F. e Matteo  hanno ipotizzato tutte la lampadine spente all'accensione dell'interruttore, dopo due secondi hanno previsto l'accensione della verde, dopo 3 secondi l'accensione della rossa, dopo 5 secondi dell'arancione, dopo 6 secondi l'accensione della blu.....

Matteo

Quindi avete ipotizzato 3 diverse modalità di accensione.

In questo gioco di luci si possono individuare varie successioni temporali, a seconda del colore di lampadina considerato, o a seconda che si considerino una tipologia di lampadina alla volta, o due, o tre o tutte.

Stamani , prendendo in considerazione l'ipotesi di accensione elaborata da Morgana, Filippo, Marco M., Leonardo, Azzurra e Lara, abbiamo individuato la seguente successione:

Almeno una lampadina accesa:

0 | 2 3 4 5 6 |  8 9 10  | 12 |  14 15 16| 18 | 20 21 22 | 24 25 26 27 28 | 30 | 32 33 34 35 36 | 38 39 40 | 42 | 44 45 46 | 48 | 50........

1. Come mai alcuni numeri vengono saltati? 
2. A cosa corrispondono dal punto di vista matematico?
3. Quali altre successioni puoi individuare?

Stamani abbiamo individuato molte altre sequenze temporali:

Lampadine verdi accese:

0 2 4 6 8 10 12 14 16 18 20 22 24.... ovvero i multipli di 2

Lampadine rosse accese:

0 3 6 9 12 15 18 21 24 27......ovvero i multipli di 3

Lampadine arancioni accese:

0 5 10 15 20 25 30 35 40 45 50....ovvero i multipli di 5

Lampadine blu accese:

0 6 12 18 24 30 36 42 48 54....ovvero i multipli di 6

Lampadine tutte accese

0 30 60 90 120 150 180 210......ovvero multipli di 30

Ci siamo chiesti: 

1. Che cosa rappresentano da un punto di vista matematico i multipli di 30 nell'ultima sequenza?
2. Cosa rappresenta il numero 30?

La serie di FIBONACCI è la risposta ad un problema  che chiedeva come una famiglia di conigli potesse accrescersi in circostanze ideali

Supponiamo di avere una coppia di conigli: maschio e femmina. I conigli possono riprodursi ad 1 mese di vita e alla fine del secondo mese una femmina può partorire un'altra coppia di conigli (supponiamo che siano un maschio e una femmina). Nello schema sottostante è rappresentato come si accresce la famiglia:

(Disegno tratto da : www.archweb.it) Perché si parla di circostanze ideali? Quante coppie ci saranno dopo 1 anno?

Leonardo Pisano, detto Fibonacci, fu un famoso matematico che visse dal 1170 al 1240
E' l'inventore della famosa serie di Fibonacci. 
Eccola:

1 - 1 - 2 - 3 - 5 - 8 - 13 - ...

Con quale criterio è costruita questa sequenza e come continua?


Sai mettere in relazione la sequenza di Fibonacci con il disegno sottostante?

Che cosa ti fa venire in mente la spirale rappresentata nel seguente disegno?

Oggi (venerdì) molti di voi hanno scoperto il criterio della serie di Fibonacci e hanno continuato la successione.....Bravi!

Vi stupirà sapere i numeri di Fibonacci sono molto ricorrenti in natura. 
Provate a contare i petali dei fiori: l'iris ne ha 3; il biancospino, la fragola... ne hanno 5, le primule, i ranuncoli, le rose selvatiche ne hanno 8, il crisantemo campestre, la cineraria il senecione di san girolamo... ne hanno 13, l'aster, l'indivia...ne hanno 21, la piantaggine, il piretro....34, i girasoli 34, 55 o 86........
E l'esempio dei petali dei fiori non è il solo!!!

Molti di voi hanno anche scoperto che esiste una corrispondenza fra i numeri di Fibonacci e la misura dei lati dei quadrati che formano il rettangolo. Bravi!

Alessandro osservando la spirale disegnata all'interno del rettangolo ha detto che gli ricorda il guscio di una chiocciola.
Ed ha ragione!!!

La sezione del guscio di un mollusco (Nautilus) ha esattamente quella forma. 




 Ma in natura ci sono tanti altri esempi riconducibili a quella forma: le corna dell'ariete, la disposizione delle scaglie dell'ananas, la disposizione dei semi nel fiore del girasole, le brattee delle pigne.........

Eccone un'altra!!!!

1. Quanti triangolini contiene la figura n° 30?
2. la figura con 200 triangolini appartiene alla sequenza? giustifica la tua risposta.

BRAVI!!!!! 

Complimenti a:

Tiziana

Rebecca

Morgana

Jivini

Lara

Tommaso F.

che oltre ad aver dato la risposta giusta all'ultima sequenza, l'hanno anche giustificata indicando strategie diverse, ma ugualmente valide.

In sintesi:

dove n rappresenta un numero dell'insieme N (numeri naturali o interi): 1  2  3  4  5  6  7  8  9  10...........

Complimenti a tutti coloro che hanno dato la risposta giusta e in particolare a chi ha trovato le parole più appropriate per giustificarla!


Visto che state diventando esperti ve ne propongo un'altra...

1. La figura numero 10 quanti triangolini contiene?
2. Una figura con 200 triangolini può appartiene a questa sequenza? Giustifica la risposta.

Complimenti a tutti quelli che hanno dato la risposta giusta, un elogio particolare va a Filippo Marcheschi che ha spiegato anche il procedimento.

Ecco una nuova sequenza!

Il triangolo formato da 30 triangoli uguali a quello di fig.1 appartiene alla sequenza? Giustifica la tua risposta.

(Fonte Invalsi)